Induced Electric Field

A conducting ring of radius $a$ is kept in $x-y$ plane with its centre at origin. A time varying magnetic field given by $\overrightarrow{B}=B_{0}t\left(-\hat{\mathrm{k}}\right)$ is applied in this region. An ideal voltmeter is connected between two points of the ring in two different cases as shown.

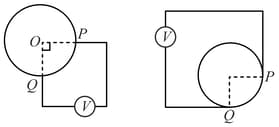
If $\pi B_0{a}^2=8 \mathrm{V}$ and voltmeter reading in case I and case II is $V_I$ and $V_{ll}$ respectively, then

As shown, a uniform magnetic field $B$ pointing out of paper plane is confined in the cylindrical region of cross-section radius r. At a distance $R$ from the center of shaded area there is point particle of mass m and carrying charge $q$. The magnetic field is then quickly changed to zero. The speed of particle just after magnetic field reduces to zero is?

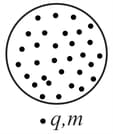
Take: Initial magnetic field $B = 6T$
Charge $q = 80 mC$
Radius $r = 5\mathrm{cm}, R = 10\mathrm{cm}$
Mass of particle $= 2 \mathrm{gram}$.

The figure shows the cross section of a cylindrical region of radius $R$ in which the magnetic field points into the page. The magnitude of the field is $1 \mathrm{T}$ at time $t=0$ and it decreases to zero in $20$ seconds.

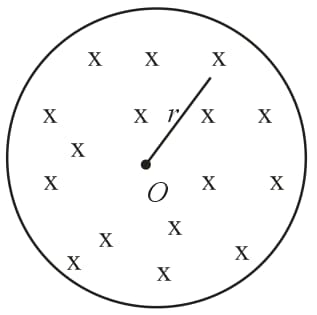
The induced electric field at a distance $r$ from the centre $O$ inside the cylindrical region is given by

A thin non-conducting ring of mass $m$ and radius $a$ currying a charge $q$ can rotate freely about its own axis which is vertical. At the initial moment the ring was at rest in horizontal position and no magnetic field was present. At instant $t=0$, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law $B=B_{0}t$. Neglecting magnetism induced due to rotational motion of ring.

Angular acceleration of the ring is:

The circular wire in figure below encircles solenoid in which the magnetic flux is increasing at a constant rate out of the plane of the page.

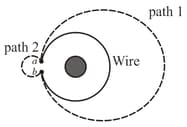
The clockwise emf around the circular loop is ${\epsilon }_0.$ By definition a voltammeter measures the voltage difference between the two points given
by $V_b-V_a=-{\int }_a^b\overrightarrow{E}·\mathrm{d}\overrightarrow{s}.$ We assume that $a$ and $b$are infinitesimally close to each other. The values of $V_b-V_a$ along the path $1$ and $V_a-V_b$ along the path $2,$ respectively are

A uniform but time-varying magnetic field $B\left(t\right)$ Exists in a circular region of radius $\text{'}a\text{'}$ And is directed into the plane of the paper, as shown. The magnitude of the induced electric field at point $P$ At a distance $r$ From the centre of the circular region

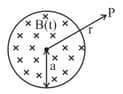
Figure shows a uniform magnetic field $\mathrm{B}$ confined to a cylindrical volume and increasing at a constant rate. The instantaneous acceleration experienced by an electron placed at $\mathrm{P}$ is-

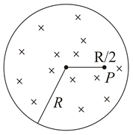
A solenoid of radius $R$ and length $L$ has a current $\mathrm{I}={\mathrm{I}}_0 \cos \omega \mathrm{t}.$ The value of induced electric field at a distance of $r$ outside the solenoid, is:

A uniform but time varying magnetic field $B=2t^3+24t$ is represent in a cylindrical region of radius $R=2.5 \mathrm{cm}$ as shown in fig.

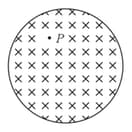
The force on an electron at $P$ at $t=2\sec .$ is

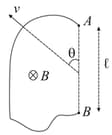
Figure shows an irregular shapped wire $AB$ moving with velocity $v.$ Find the emf induced in the wire :-

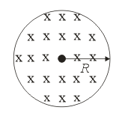
As shown in the above figure, there is a uniform magnetic induction $B$ parallel to the axis of a cylindrical space of radius $R$. Plot the graph between the induced electric field and distance $r$ from the axis of the cylinder, if it is known that the rate of change of magnetic induction is constant.

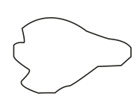
As shown in the above figure, consider a closed-loop held in a magnetic field. The change in the magnetic flux linked with the loop induces a voltage $V$ in the loop. Now, find the work done in taking a charge $Q$ over a complete loop:

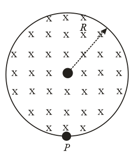
Consider a cylindrical region of radius $R$, where a uniform magnetic field of induction $B$ is confined. At point $P$, a negative charge of magnitude $e$ is placed. Find the acceleration of the charge, if $\frac{\mathrm{d}B}{\mathrm{d}t}=C$, where $C$ is a constant.

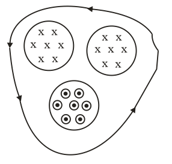
As shown in the above figure, a loop surrounds three regions of the magnetic field where the magnitude of the magnetic field is decreasing at a constant rate $\alpha$. Take the area of each region as $A$. Now find the $\oint \overrightarrow{\mathit{E}}\mathit{.}\overrightarrow{\mathit{d}\mathit{l}}$ along the given loop, where $\overrightarrow{\mathit{E}}$ is the induced electric field.

Consider the uniform magnetic field of magnitude $0.01 \mathrm{T}$ directed perpendicularly to the plane of a conducting ring of the radius $1 \mathrm{m}$. If the ring is oscillating with a frequency of $0.1 \mathrm{kHz}$, then find the induced electric field.

Consider a $q$ charged ring of radius $b$ and mass $m$ in $x\mathit{-}y$ plane with its centre at the origin. There is a magnetic field $B$ which is confined to a region $r\le a$ and points out of the paper. Here, $r=0$ is origin and $a<b$. If this magnetic field is brought to zero in time $\text{Δ}t$, then find the angular velocity of the ring after the field vanishes,

A thin non-conducting ring of mass $m$ and radius $a$ carrying a charge $q$ can rotate freely about its own axis which is vertical. At the initial moment the ring was at rest in horizontal position and no magnetic field was present. At instant $t=0$, a uniform magnetic field is switched on which is vertically downward and increases with time according to the law $B=B_{0}t$. Neglecting magnetism induced due to rotational motion of ring.

Angular acceleration of the ring is:

A parabola $\mathrm{y}=\mathrm{k}{\mathrm{x}}^2$ shaped wire is placed in aperpendicular uniform magnetic field of induction B. At $\mathrm{t}\mathrm{ }=\mathrm{ }0$, wire starts moving from the vertex O with a constant acceleration linearly as shown in figure.Then emf induced in the loop will be-

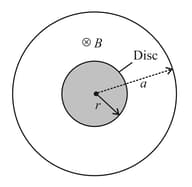
A uniform disc of radius $r$ and mass $\mathrm{m}$ is charged uniformly with the charge $q$. This disc is placed flat on a rough horizontal surface having coefficient of friction $\mu$. Find the time in second after which the disc begins to rotate when a uniform magnetic field is present in a circular region of radius a $(>r)$ but varying as $k{t}^3$ as shown in figure. (Given $r=1 \mathrm{m}, m=18 \mathrm{kg}, \mu =0.1, k=4, g=10 \mathrm{m} {\mathrm{s}}^{-2}$). $$$$

There is a non conducting ring of radius $R$ and mass m having charge $q$ uniformly distributed over its circumference. It is placed on a rough horizontal surface. A vertical time varying uniform magnetic field $B=4t^2$ is switched on at time $t=0$. The coefficient of friction between the ring and the table, if the ring starts rotating at $t=1\sec$, is